在運動學裏，歐拉旋轉定理（Euler's rotation theorem）表明，任意三維空間的旋轉皆可簡單表示為對於某一固定軸的旋轉。
也就是說任意的旋轉，都可以由固定軸 + 旋轉角度所組成，也就是軸角表示法(Axis-Angle Representation)。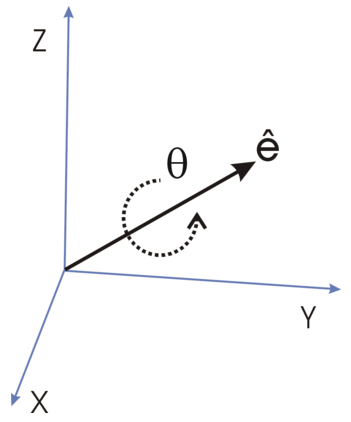

而這裡就讓我們介紹cv :: Rodrigues的用法。
根據stackoverflow的這篇討論到opencv在旋轉向量的表示並不是透過[角度Θ,x,y,z]角度搭配一個旋轉軸表示。
而是更緊湊的只用了x,y,z三個元素的向量，角度的部分則是使用了這個向量的長度做為代替。
https://stackoverflow.com/questions/12933284/rodrigues-into-eulerangles-and-vice-versa
solvePnP 可以用在相機校正求取相機的外方位參數用，或是日後評估相機運動其中一種方式。

旋轉角度theta是輸入向量的模長 theta = sqrt(a^2 + b^2 + c^2)
旋轉軸v是標準化的輸入向量：v = rod2/theta = [a/theta, b/theta, c/theta]

接下來我們就能透過昨天生成的旋轉矩陣轉換成旋轉向量，再將轉換出來的旋轉向量轉回旋轉矩陣，比較兩者其結果是否有差異。

	std::cout <<"result1\n"<< rotation_y* rotation_x* rotation_z << std::endl;

	cv::Mat result = rotation_y * rotation_x * rotation_z;

	cv::Mat rotation_vector;
	cv::Rodrigues(result, rotation_vector);

	cv::Mat compare_result;
	cv::Rodrigues(rotation_vector, compare_result);

	std::cout << "compare_result\n" << compare_result << std::endl;

總結:尤拉角是依順序對三個不同的XYZ軸旋轉的角度的描述，其中軸的順序有其意義並不能隨意交換。
而旋轉向量通常是一個旋轉軸[x,y,z]搭配一個角度，比較特殊的表示方式例如openCV則是只用了三個元素來表示，
其中角度的部分則用向量的長度取代。
雖然兩種方式都可以只用三個元素來表示旋轉但其意義截然不同。